Остаток от деления в Python

Полное руководство про остаток от деления и его практическое применение в программировании на Python и базах данных.

Оглавление

1. Смысл остатка от деления
2. Остаток от деления в Python
3. Остаток от деления на 3

Популярные приёмы

1. Деление на группы
2. Проверка на четность
3. Вычисление последней цифры числа
4. Форма множественного числа
5. Округление до целых (до тысяч)
6. Получение секунд и минут
7. Текущее состояние
8. Зацикливание
9. Сдвиг
10. Контрольные числа
11. Прочие алгоритмы
12. Отрицательный остаток от деления

Само понятие «остаток от деления» довольно простое и его изучают в начале средней школы.

Тем не менее в программировании бывает не очевидно, когда и как им пользоваться. Особенно новичкам. При этом сфер применения остатка от деления очень много и в этой статье мы разберем 10 самых популярных приёмов, а те, кто дочитает до конца, бонусом узнает про 11 способ, о котором не знают даже профессиональные разработчики.

Смысл остатка от деления

Перед тем, как начнем, сперва освежим школьные знания и разберемся, что такое остаток от деления. Для примера я возьму трёх человек и шесть яблок:

Моя задача — разделить эти яблоки между всеми участниками поровну. И говоря об остатке от деления надо сразу обозначить два правила:

1. Во-первых, делить надо поровну, чтобы у каждого из участников было одинаковое количество яблок.
2. Во-вторых, мы не можем резать яблоки. Мы можем давать только целые.

И в случае 6-и яблок, каждому участнику достается ровно по 2. У меня же яблок не остается, а следовательно остаток от деления равен нулю:

Если яблок будет 5, то каждому достанется по одному. А у меня останется 2:

Два яблока я никак не смогу разделить поровну между тремя участниками. Резать я их не могу в соответствии со вторым правилом. А если я продолжу их делить, то кто-то останется без яблока (а это нарушение первого правила).

И собственно остаток от деления 5-и яблок на трёх участников равен двум.

Если яблок будет 7, то каждый получит по два яблока и одно останется у меня. Остаток деления 7-и на 3 равен единице.

В этом и заключается весь математический смысл остатка от деления. Теперь переключимся к программированию на Python.

Остаток от деления в Python

В компьютерных программах остаток от деления записывается либо с помощью процента % либо с помощью оператора mod, либо с помощью функции mod(), которая в скобках принимает два параметра.

Первый способ, с помощью процента %, поддерживается всеми современными языками программирования, включая Python, PHP, Java и JavaScript:

# Python
print(7 % 3)
1

Оператор mod вы можете встретить в Pascal, а также в математических статьях и описаниях алгоритмов.

7 mod 3 = 1

Функцию mod() вы можете встретить в SQL:

# SQL
SELECT 
    mod(7, 3) as modulus1  -- вернет 1
    7 % 3 as modulus2      -- вернет 1

Далее в статье я буду использовать % как самый популярный способ представления остатка от деления и давайте разбираться как его использовать в программах на Питоне.

Если вы хотите научиться программировать на Python, то ждём вас на нашем курсе по Python.

Остаток от деления на 3

Сперва посмотрим на такую таблицу:

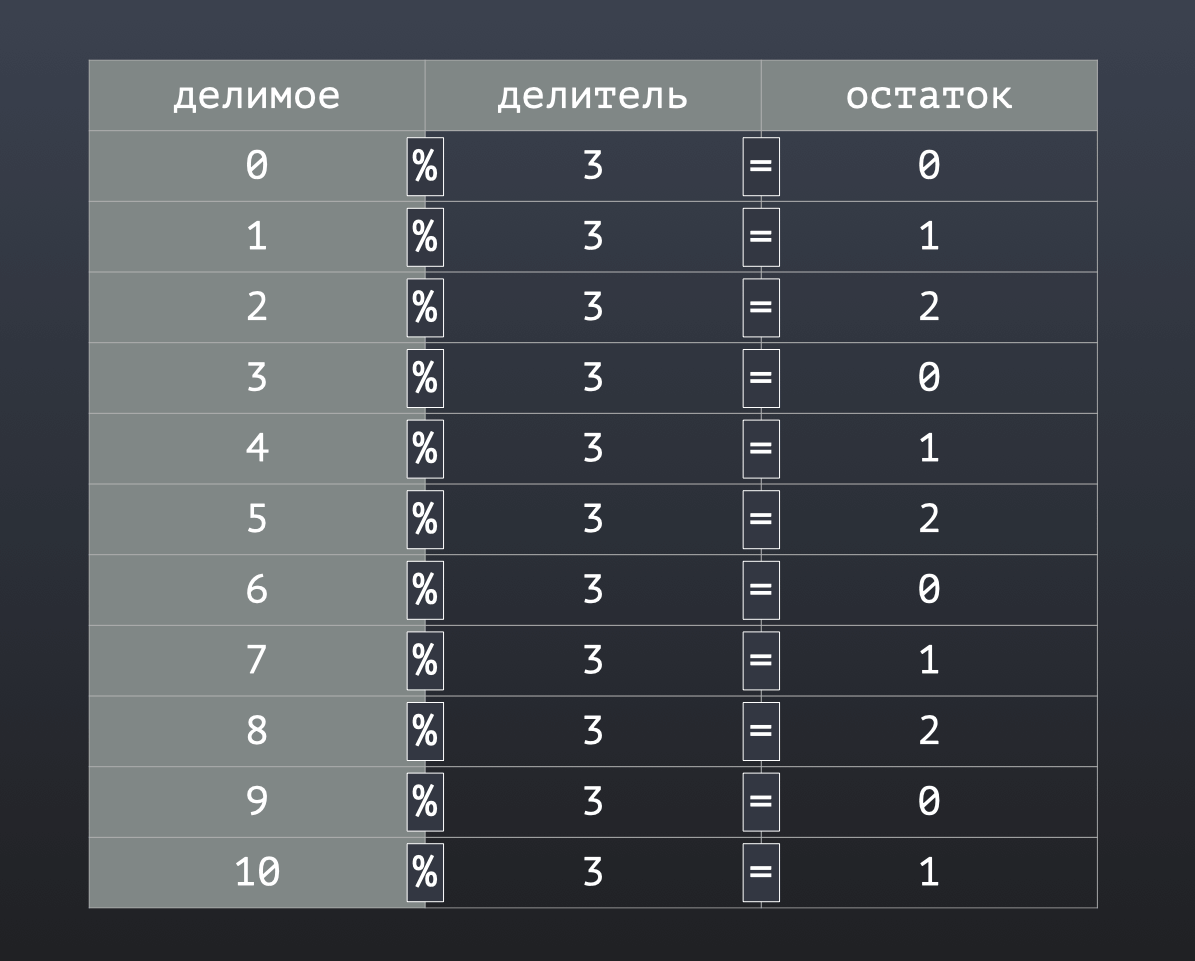
В ней слева я проставил числа от нуля до 10 и это будут наши яблоки, которые мы хотим разделить.

В средней колонке я обозначил количество участников, между которыми эти яблоки нужно делить. Пусть сперва будет 3.

Справа же будет стоять остаток от деления на 3 и давайте поговорим о его особенностях.

Во-первых, все значения остатка находятся в диапазоне от нуля до двух. Иными словами, остаток от деления на 3 всегда будет меньше трёх.

Если мы будем делить яблоки между пятью участниками, то остаток будет в диапазоне от нуля до четырех. То есть меньше пяти. Это логично, ведь если мы делим 10 яблок на пятерых и у нас останется более 4-х яблок, например 5, то мы можем запустить следующий круг деления и раздать остаток всем поровну.

Именно поэтому, остаток всегда будет меньше, чем делитель, то есть чем количество человек, на которое мы делим.

Но вернемся к остатку от деления на 3 и посмотрим на второе свойство, которое заключается в том, что если в правом столбце у нас стоят натуральные числа, которые возрастают на единицу: 0, 1, 2, 3, 4, 5 и до бесконечности, то остаток от деления будет зациклен 0-1-2, 0-1-2, 0-1-2 и так далее.

И зная такие особенности поведения остатка от деления мы можем применить его в программировании.

1. Деление на группы

И первое применение – это деление чего-либо на группы.

Давайте раскрасим строки нашей таблицы разными цветами. Отталкиваться будем от значения остатка от деления. Так для нуля возьмем желтый. Для единицы оранжевый, а для двойки оставим как есть. Итого у нас получилось три группы разных цветов:

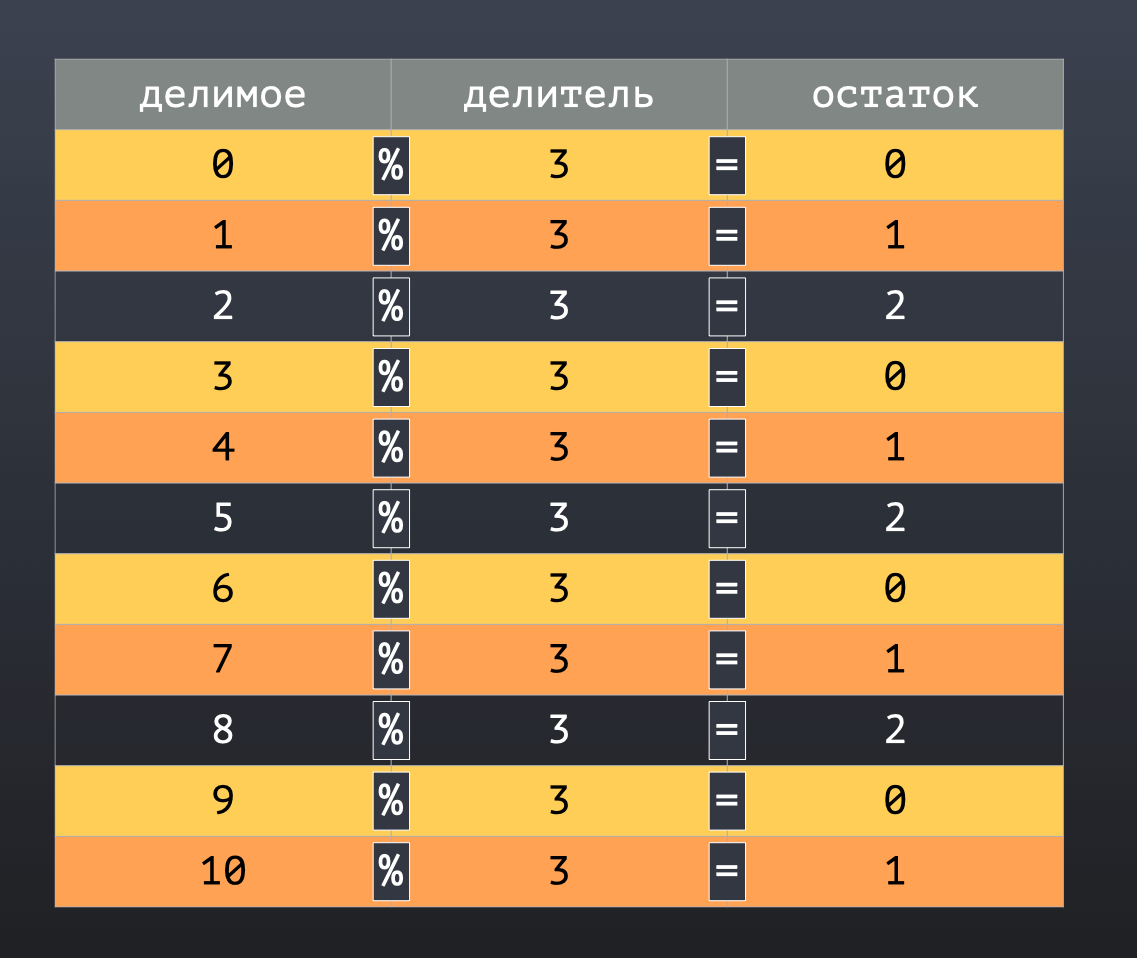
И теперь мы можем каждой группе, например, отправить своё рекламное сообщение. То есть желтым отправляется желтое письмо, оранжевым - оранжевое, а темным - темное.

И если желтая группа покажет лучшую конверсию (больше всего купит товара или перейдет по ссылке), то далее мы сможем использовать эти рекламные материалы на более широкой аудитории.

Такой приём, когда мы тестируем разные рекламные материалы на разных группах, называется AB-тестом и он активно используется в маркетинге.

Сперва протестировали на небольшом наборе, а затем лучший вариант отправили в массы.

Если у вас всего два варианта, то нужно будет взять остаток от деления на 2 и получить разбитие на две группы.

Единственное условие, чтобы числа в левой колонке шли друг за другом без пропусков. Но это несложная задача на любом языке программирования.

1.2 Деление на группы пополам

Давайте поговорим, почему подход с цикличным разделением на группы, лучше, чем подход, когда мы просто делим некую таблицу или некий набор данных пополам:

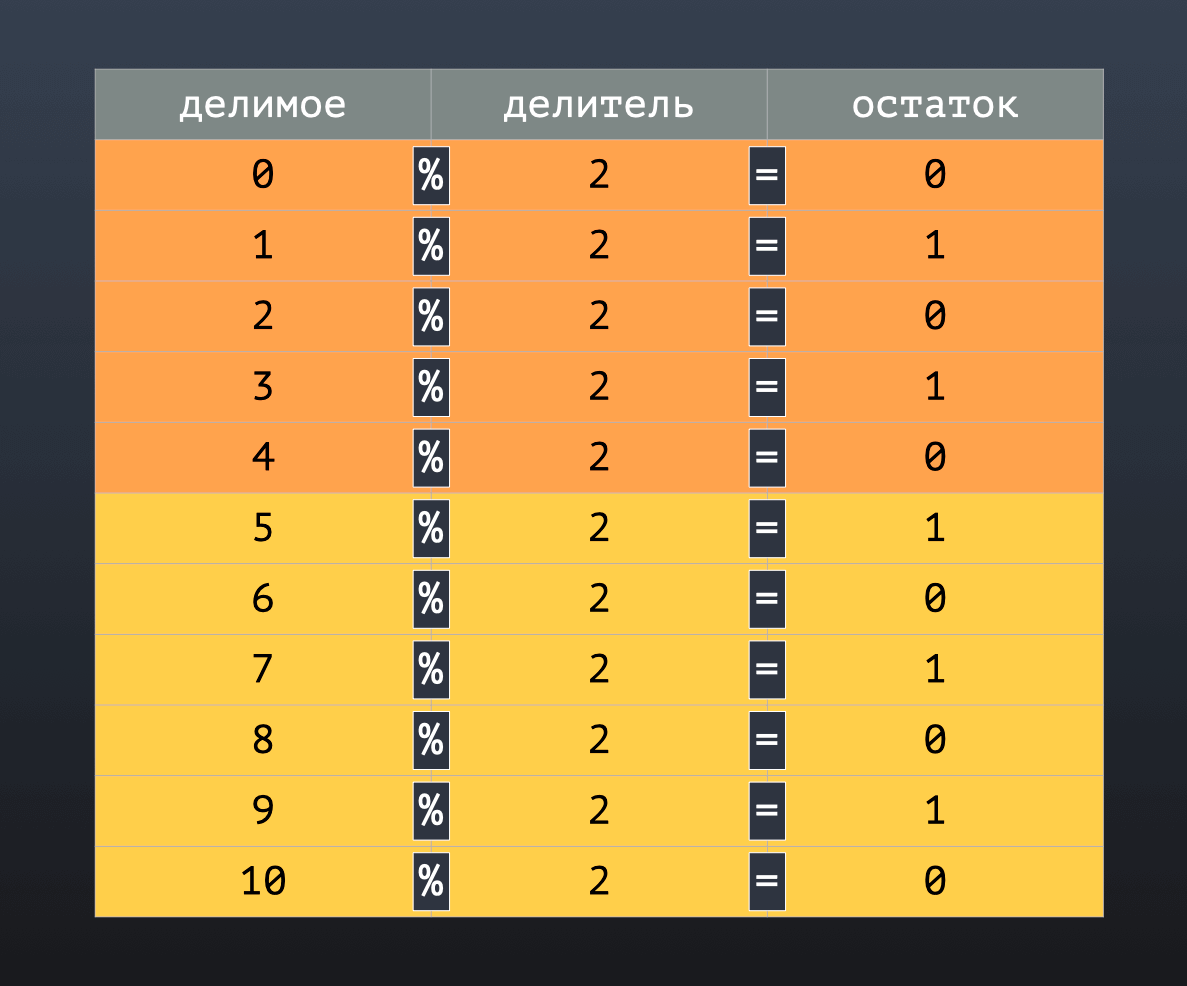
Представим, что это база данных пользователей. И если наш проект работает продолжительное время, то пользователи в верхней части таблицы зарегистрировались давно (может быть год, два или даже 5 лет назад), а в нижней недавно (сегодня, вчера и так далее).

И вот если мы сделаем рассылку с такой разбивкой, то группы покажут разные результаты не потому, что, они получили разные рекламные сообщения, а потому что старые пользователи будут совсем по-другому относиться к вашему проекту, нежели новые.

А вот цикличное разделение нивелирует этот момент и добиться его можно как раз с помощью остатка от деления: на 2, на 3, на 4 или сколько угодно. В зависимости от того, сколько групп вам нужно.

1.3 NTILE

Такое деление на группы в языке SQL можно осуществить как с помощью остатка от деления, так и с помощью оконной функции NTILE. И если мы посмотрим в исходные коды MySQL, которые написаны на C++, то внутри функции NTILE найдем вот такую строку:

int64 modulus = m_window->last_rowno_in_cache() % buckets;

В ней слева стоит некий счетчик (m_window->last_rowno_in_cache()), который перебирает значения 1, 2, 3 и так далее, а справа количество групп (buckets), на которые делим. И, разумеется, между ними остаток от деления. Всё точно так же, как в нашем примере.

Кстати, слово buckets, которое используется для обозначения количества групп, с английского языка переводится как «вёдра». И такое имя часто используется в книгах по алгоритмам, а также в реальных программах, где нужно разбить что-то на группы. Или, другими словами, разбить по вёдрам, положить каждое яблоко в своё ведро. Можете использовать buckets и вы.

Что ж, с оконной функцией NTILE мы закончили. Кстати, если вы хотите научиться работать с оконными функциями в SQL, то у нас есть отличный продвинутый курс по SQL, где мы в деталях разбираем окна, транзакции, хранимые процедуры и другие возможности работы с базами данных.

2. Проверка на четность

Но вернемся к остатку от деления на 2 и еще раз взглянем на таблицу:

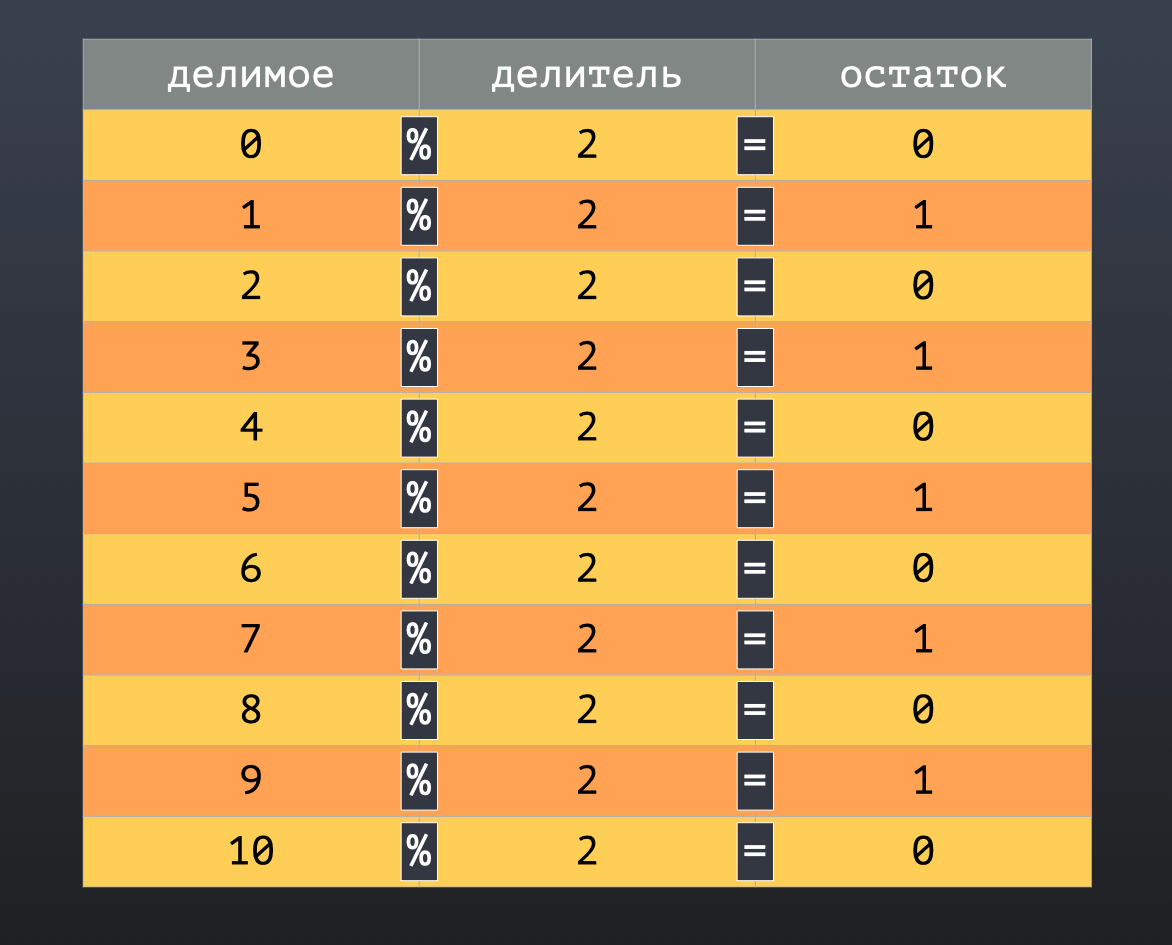
Обратите внимание, что у четных чисел (желтых) остаток равен нулю, а у нечетных единице. И собственно остаток от деления на 2 – это отличный маркер того, четное перед нами число или нет.

Простейший код на Python выглядит так:

if число % 2 == 0:
    # четное
else:
    # нечетное

3. Вычисление последней цифры числа

Также остаток от деления используется для вычисления последней цифры числа. Возьму, например, 134. И для того, чтобы получить последнюю цифру, нам нужно взять остаток от деления на 10, так как у нас десятичная система счисления.

print(134 % 10)
4

Последняя цифра любого числа всегда меняется в диапазоне от 0 до 9, других вариантов быть не может. И собственно остаток от деления 134 на 10 – это четыре. А 1456 на десять – это 6.

print(1456 % 10)
6

Теперь возьмем пример посложнее. Представим, что нам нужно получить две последние цифры числа. То есть из 134 выделить 34. И обратите внимание, что последние две цифры всегда будут в диапазоне от нуля до 99. Всего 100 значений.

Следовательно, остаток от деления 134 на 100 будет равен 34. Для 1456 мы получим 56. И так далее.

print(134 % 100)
34
print(1456 % 100)
56

Добавляя ноль к делителю, мы сможем отрезать от числа всё большие и большие части.

4. Форма множественного числа

И такой приём используется в программах для получения формы множественно числа.

Возьмем слово «банан» и понаблюдаем как меняется его окончание.

0 бананов
1 банан
2 банана
3 банана
4 банана
5 бананов
6 бананов
7 бананов
8 бананов
9 бананов

Если изучить список, то можно выделить три группы с разными окончаниями (нулевое, -а и -ов) и это справедливо для большинства слов русского языка.

Выбор каждого конкретного окончания зависит от того, какая цифра стоит в конце числа.

Возьмем 157, остаток от деления на 10 будет равен семи, а значит нам нужно использовать слово «бананов» – «157 бананов». По этому же принципу можно получить и другие варианты окончаний.

Правда имейте в виду, что это упрощенный пример, так как, в диапазоне от одиннадцати до четырнадцати должна быть использован вариант «бананов», но это решается несложным вычислением остатка от деления на 100.

То есть с помощью остатка от деления на 100 мы получаем две последние цифры числа и проверяем не лежат ли она в диапазоне от 11 до 14. В остальных случая мы используем остаток от деления на 10 для того, чтобы получить последнюю цифру и выбрать соответствующую группу.

Код на Python выглядит примерно так:

variants = ["банан", "банана", "бананов"]
bananas = 12

if bananas % 100 >= 11 and bananas % 100 <= 14:
    variant = variants[2]
elif bananas % 10 == 1:
    variant = variants[0]
elif bananas % 10 >= 2 and bananas % 10 <= 4:
    variant = variants[1]
else:
    variant = variants[2]

print(f"{bananas} {variant}")

Возможно есть еще какие-то правила, но в целом логику вы уловили.

5. Округление до целых (до тысяч)

Такой же подход можно использовать для округления до десятков, сотен или тысяч. Представим, что нам нужно из 134 456 получить просто 134 000. И для этого достаточно написать вот такую формулу:

print(134456 - 134456 % 1000)
134000

В правой части мы получаем 456 и далее вычитаем это число из начального значения, что и даёт финальный результат.

Соответственно если мы возьмем другое число и применим те же действия:

print(13196 - 13196 % 1000)
13196

то получим чистые 13 100. Как видите, довольно просто.

Пример такого округления можно увидеть, когда вы переходите в админку YouTube:

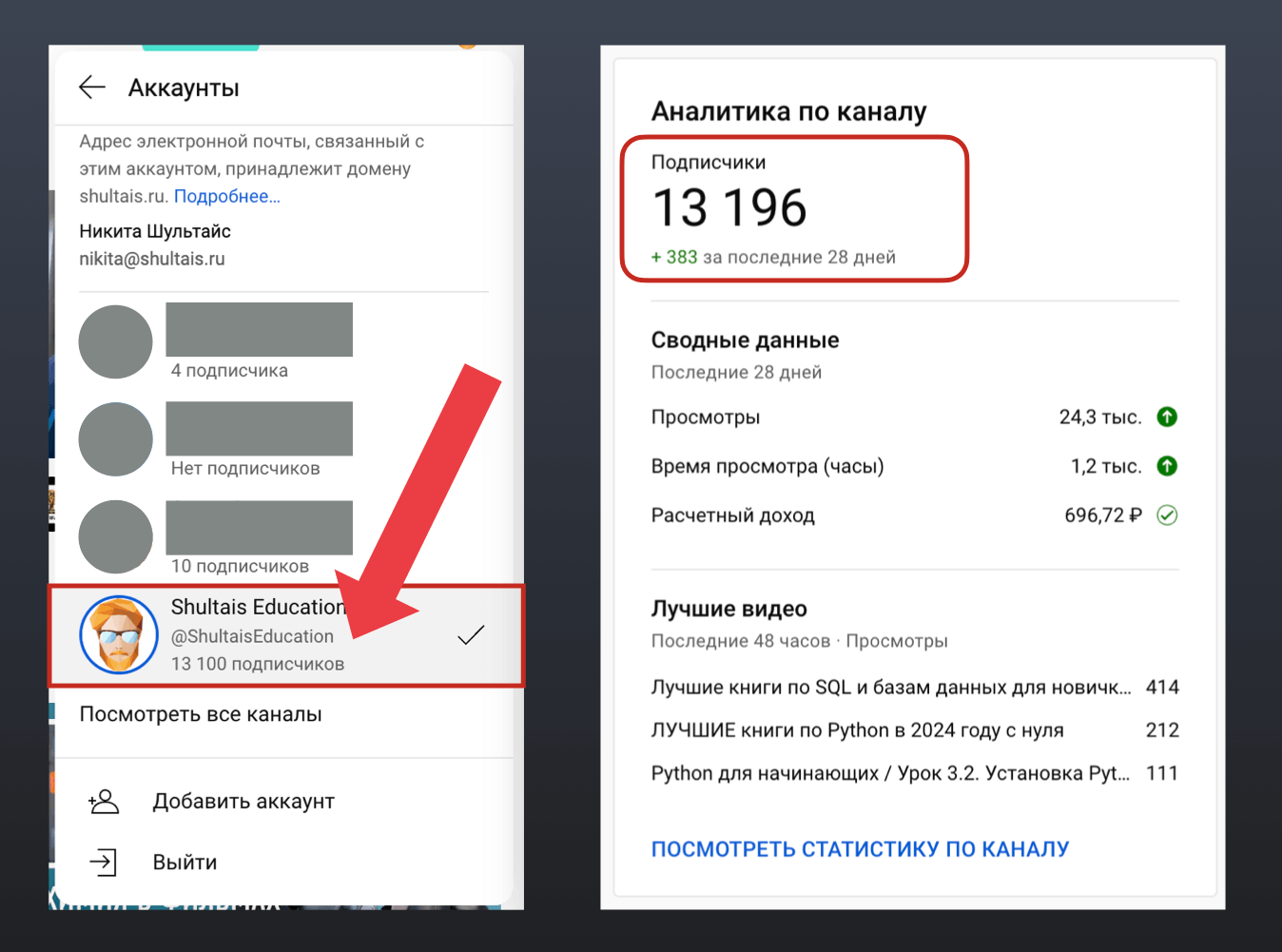
Так у меня в выпадающем меню показывается 13100 подписчиков, но при этом реально их 13196. Приёмы, которые мы рассматриваем в этой статье не выдуманные, а вполне реальные.

6. Получение секунд и минут

Подход, который мы рассмотрели выше, также применятся при работе со временем: секундами, минутами, часами, днями и так далее. Ведь там тоже есть цикличность. Так, секунды и минуты лежат в диапазоне от 0 до 59, а часы от 0 до 23.

И все эти параметры перманентно зациклены с момента большого взрыва. А если есть какая-то цикличность, то это повод задуматься об остатке от деления.

Возьмем довольно популярную задачу, когда нам даётся полное количество секунд, пусть будет 271, и нам нужно вычислить сколько прошло целых минут и сколько осталось секунд.

И если мы возьмем остаток от деления 271 на 60, то получим 31 секунду.

А далее мы можем из 271 вычесть 31 и просто разделить на 60, что даст нам 4 целых минуты.

total_seconds = 271

seconds = total_seconds % 60
minutes = int((total_seconds - seconds) / 60)

# Можно сразу написать так
minutes2 = total_seconds // 60

print(f"{minutes:02}:{seconds:02}")
print(f"{minutes2:02}:{seconds:02}")

То есть 271 секунда содержит в себе 4 минуты 31 секунду. Такой логикой можно вычислять время для самых разных промежутков. Полное количество минут, часов, дней и так далее. Арифметика тут элементарная, главное правильно расписать порядок формул.

Перед тем как двигаться дальше, давайте посмотрим на наш пример немного в другой плоскости.

6.1 Перенос к конечному состоянию

Итак, у нас есть некая непрерывная прямая с повторяющими событиями. В нашем случае это минуты, которые меняются каждые 60 секунд:

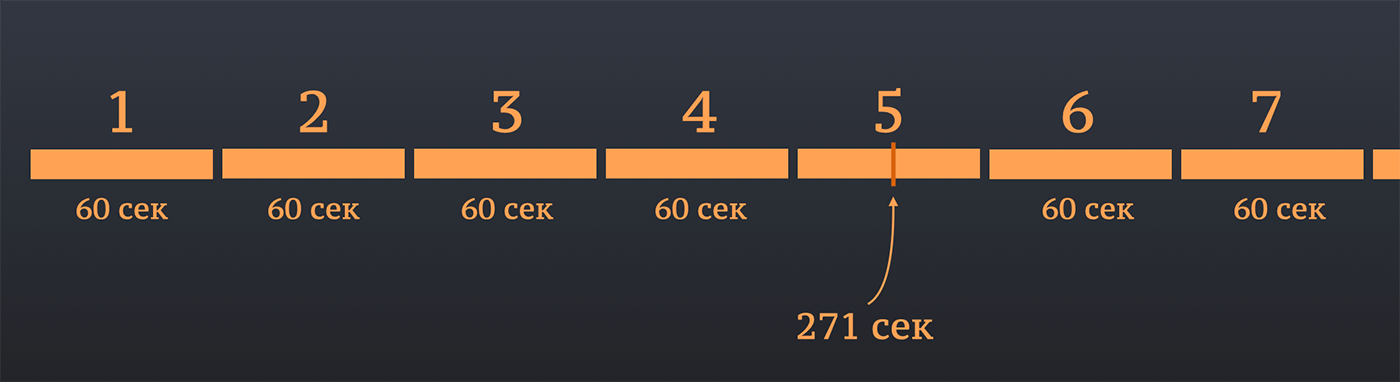
На этой прямой мы отмечаем некое значение – 271 и нам нужно узнать сколько секунд прошло в последнем промежутке - в пятом.

Фактически нам нужно избавиться от всех завершенных минут в прошлом. То есть те минуты, которые уже полностью закончились, нужно вырезать и оставить только финальный отрезок:

И вот как раз остаток от деления, как бы убирает всё целое, и сразу переносит нас в некое текущее состояние, в котором осталась 31 секунда. И такие переносы в незавершенные части (в остатки) открывают для нас еще один класс задач.

7. Текущее состояние

Представим, что у нас есть светофор, который 4 секунды горит зеленым и 2 секунды красным. Вот мы его включили и нам нужно узнать, какой свет будет через 3 секунды после начала:

Очевидно, что это зеленый. Через 4 секунды загорится красный. И в целом в рамках одного временного промежутка свет светофора вычислить несложно.

Это делается элементарным набором условий в любом языке программирования. Но что, если нужно получить состояние светофора, скажем, через 10 секунд.

И самый простой способ – это воспользоваться остатком от деления. Полный цикл работы светофора у нас занимает 6 секунд, а текущее время 10 секунд.

И собственно остаток от деления 10-и на 6 – это 4. Иными словами, с помощью этой операции мы пропускаем все целые (завершенные циклы) и переходим в последний незавершенный отрезок, в котором прошло 4 секунды. На четвертой секунде горит красный свет.

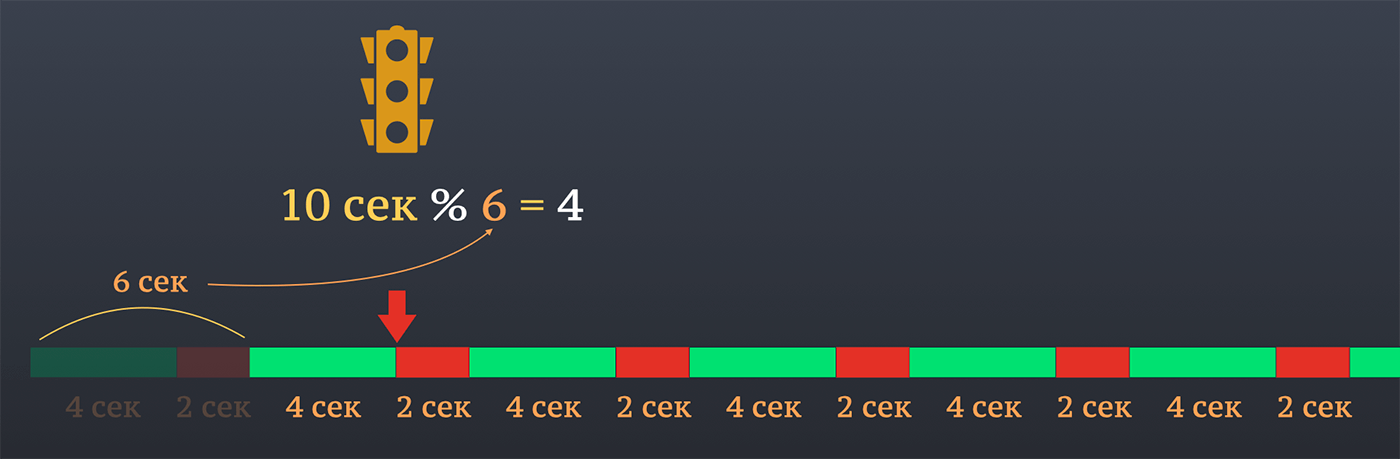
Таким способом мы можем определить состояние светофора на любой момент времени.

Прошла 271 секунда. Не проблема вычисляем остаток от деления и получаем 1. То есть горит зеленый.

total_seconds = 271

last_period = total_seconds % 6

if 0 <= last_period < 4:
    print("Зеленый")
else:
    print("Красный")

Разумеется, в рамках одного цикла работы светофора может быть спрятано сразу несколько состояний: зеленый, желтый и красный. Любой продолжительностью. Но в любом случае мы можем вычислить и общую продолжительность одного цикла, и остаток в последнем цикле.

С этим разобрались и следующее применение остатка – это зацикливание.

8. Зацикливание

Порой нам нужно читать или записывать данные из каких-то источников по кругу. Например, у нас есть некая строка символов, и мы хотели бы первый символ «A» положить в первый файл, «B» во второй, «C» в третий, «D» в четвертый. Затем «E» снова в первый и так далее по кругу.

В кокой-то момент мы дойдем до символа «J» и нам нужно вычислить тот диск или тот файл, в который его следует записать:

Для этого нам нужны 2 числа: - первое – это то, какая сейчас идет буква по номеру. Ранее мы записали 9 символов и, следовательно, у «J» будет 9 номер, если считать с нуля.

Также нам нужно знать по скольким ведрам мы распределяем наши символы. Очевидно, что по четырем.

И теперь осталось вычислить остаток от деления 9 на 4 – это будет единица. И 1 это был бы номер ведерка если бы они у нас нумеровались с нуля. Но у нас номера начинаются с единицы. И чтобы правильно вычислить нужный файл, нужно к остатку добавить 1, что в итоге даст нам 2.

j_num = 9
buckets = 4

print(j_num % buckets + 1)
2

То есть помещаем «J» во второй файл и переходим к следующей букве - «K». Для неё по нашей формуле мы получим 3 и, следовательно, «K» идет в третий бакет:

k_num = 10
buckets = 4

print(k_num % buckets + 1)
3

В целом вся техника очень похожа на ту, когда мы разбивали на группы, просто немного другая сфера приложения.

Порой, когда условия заданий лежат в другой плоскости, мы можем не заметить приёмы или паттерны, которыми умеем пользоваться. Именно поэтому я показываю пусть и похожие, но всё же немного разные примеры.

8.1 Заполнение по кругу

И конкретно на этом мы задержимся еще какое-то время. Разберем ситуацию, когда в некоем фиксированном массиве из десяти ячеек, нужно хранить строго последние поступившие данные.

Скажем, нам нужно хранить 10 последних оценок, которые поставили водителю такси и на базе этих оценок считать актуальный рейтинг.

Чтобы это реализовать нам нужен, собственно массив из 10 элементов, а также счетчик, который будет хранить номер текущей оценки. Номера считаем с единицы и до бесконечности.

Пусть первая оценка будет 5. Давайте вычислим куда её следует поместить. И так как на этот раз мы начинаем с единицы, а не с нуля, то нам нужна такая формула:

(N - 1) % 10

Номер оценки минус 1 и затем остаток от деления на десять.

Берем первую оценку, подставляем в формулу, вычисляем остаток от деления и пятерка уходит в нулевую ячейку таблицы.

num = 1
print((num - 1) % 10)
0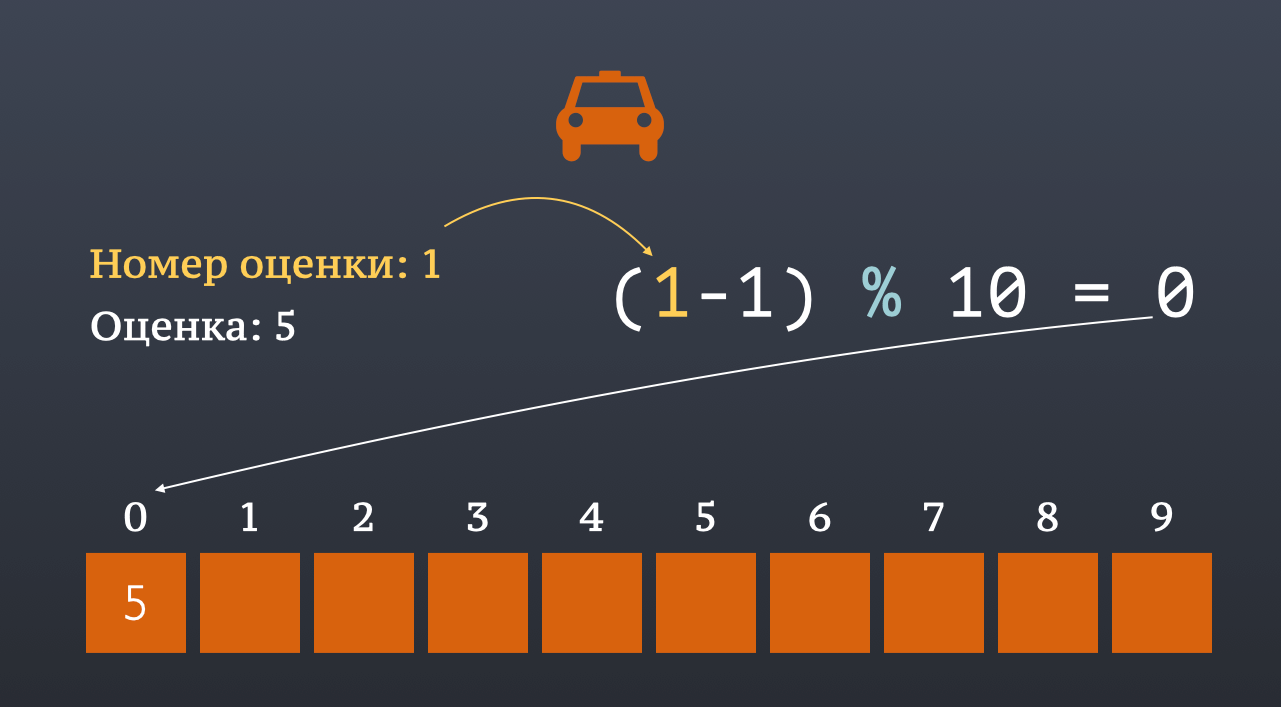

Вторая оценка снова 5, и она уходит в первую ячейку. Третья оценка идет во вторую ячейку и так далее. В какой-то момент мы заполним весь массив и сейчас в нём 10 последних оценок:

Если мы захотим поместить еще одну оценку, то самая первая будет уже неактуальна, так как мы считаем рейтинг на основе последних десяти оценок.

А значит мы смело можем поставить 11-ю оценку на нулевую позицию, заменив самые старые данные. Подставляем 11 в формулу, получаем 0 и отправляем оценку в массив.

num = 11
print((num - 1) % 10)
0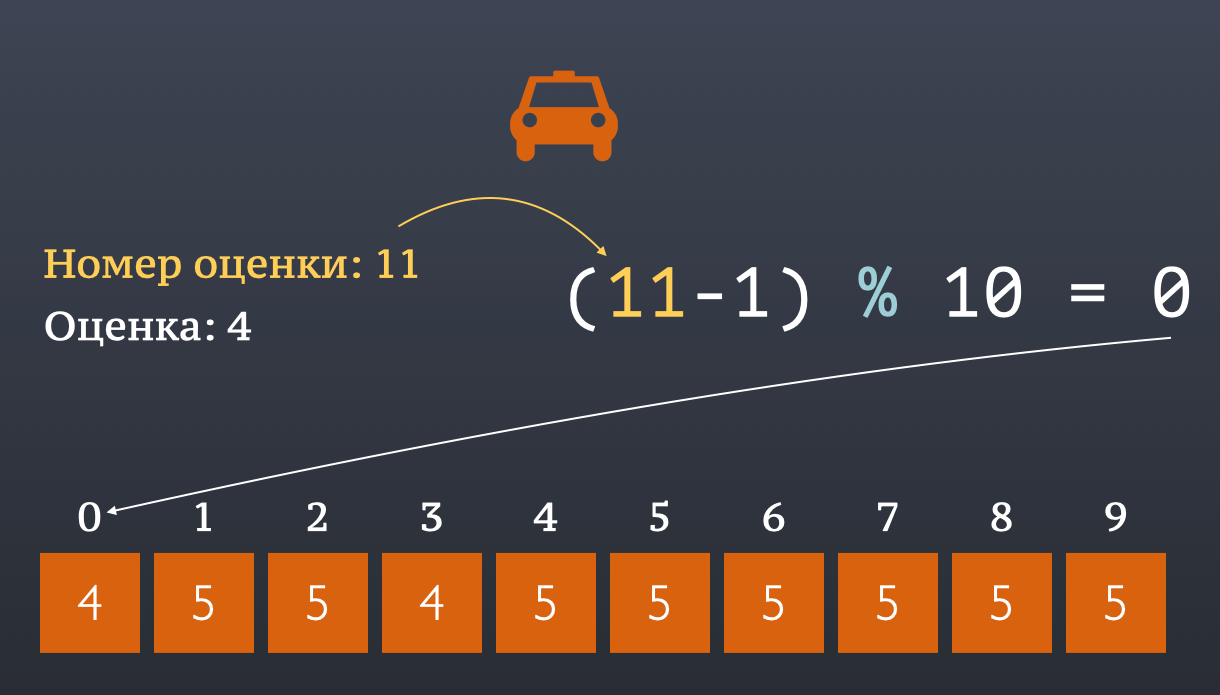

В самом массиве по-прежнему всего 10 элементов и при этом они отвечают за последние десять оценок. Иными словами, заполнение происходит по кругу. И этот приём циклического чтения или заполнения, нередко используется в реальных программах и алгоритмах.

Следующий пример, который мы рассмотрим, похож на зацикливание, но из-за другого контекста я называю его сдвигом.

9. Сдвиг

И проще всего его показать на шифре Цезаря. Суть шифра простая, мы берем некий алфавит символов. И далее сопоставляем ему точно такой же алфавит, а затем делаем сдвиг между ними. Скажем на два символа.

После, когда нам нужно зашифровать, например, символ «D». Мы просто берем вместо него «F». То есть тот символ, который расположен ниже.

Собственно задача шифровальщика – это взять каждый символ исходного текста и заменить его на соответствующий символ из нижнего алфавита.

В целом, довольно просто, но давайте посмотрим на ситуацию, когда в тексте встречается символы «Y» или «Z».

Сейчас для них символы для замены не указаны. При этом в начале строки у нас подвисли символы «AB». И чтобы сбалансировать алфавиты, нужно перенести «AB» в конец, таким образом зациклив алфавит.

И теперь каждому символу верхнего алфавита есть соответствующий символ в нижнем.

При этом нам не нужно реально составлять два алфавита. Достаточно одного (основного) плюс остаток от деления.

Всего у нас в алфавите 26 символов. Возьмем «Q» на позиции 16. Добавим к индексу два, так как сдвиг у нас равен двум. И после возьмем остаток от деления на длину алфавита.

abc_len = 26
q_pos = 16
shift = 2

new_pos = (q_pos + shift) % abc_len
print(new_pos)
18

Получили 18. И, следовательно, нам нужно заменить «Q» на символ, который находится на 18 позиции, а это «S».

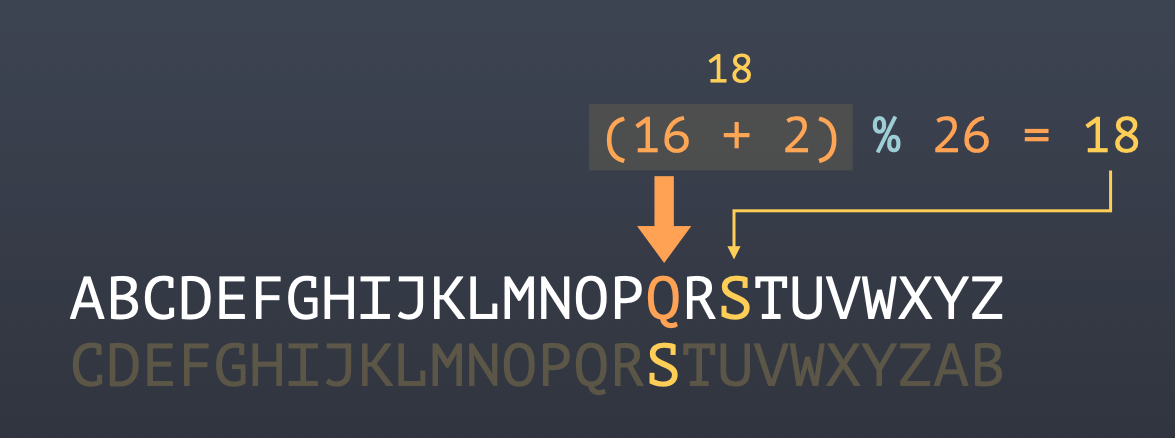
Если посмотреть на нижний алфавит, то под «Q» как раз и будет «S».

На самом деле 16 + 2 уже даёт нам 18 и, собственно, сам эффект сдвига достигается как раз сложением исходного индекса с величиной сдвига.

Вычисление остатка от деления никак на исходные 18 не влияет, так как 26 больше 18. Остаток от деления тут влияет не на сдвиг, а на цикличность. Давайте возьмем 25 букву алфавита - «Y». Если к 25 добавить 2, мы получим 27. 27 больше 26, а следовательно, тут уже срабатывает остаток от деления, который даёт нам единицу.

abc_len = 26
y_pos = 25
shift = 2

new_pos = (y_pos + shift) % abc_len
print(new_pos)
1

На позиции 1 располагается символ «A», и как раз на него нам нужно сделать замену. Что и подтверждает нижний алфавит.

Собственно, второй алфавит и не нужен. Все вычисления проводятся на основном алфавите с помощью несложной формулы — сдвиг плюс остаток от деления.

10. Контрольные числа

С основными приёмами использования остатка от деления мы разобрались, а теперь еще пару слов о том, где остаток применяется.

И начнем с вычисления контрольных чисел. Например, при формировании номера ИНН. Так ИНН физического лица содержит 12 цифр. Первые четыре, отвечают за регион, где ИНН присвоен, далее идет номер внутри региона, а вот последние две цифры вычисляются по формуле с помощью остатка от деления и их называют контрольными числами или контрольной суммой.

11-я цифра рассчитывается по такой формуле:

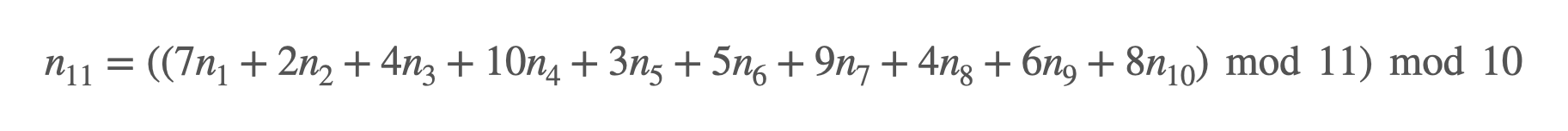
В ней берется каждая из 10 цифр основного номера, умножается на какой-то коэффициент в диапазоне от 2 до 10, всё это складывается, а после сперва берется остаток от деления на 11, а затем на 10.

11 – это простое число и оно позволяет лучше отлавливать ошибки и опечатки в номере, а остаток от деления на 10 просто приводит финальный результат к однозначному числу в диапазон от нуля до девяти. В нашем случае если мы подставим данные в формулу, то получим на выходе единицу.

Второе контрольное число рассчитывается по похожей формуле, тут мы также складываем все числа основного номера плюс добавляем в конце контрольное число, которое получили на прошлом шаге, а после снова вычисляем два остатка от деления, что даёт последнее однозначное число. Тоже единицу.

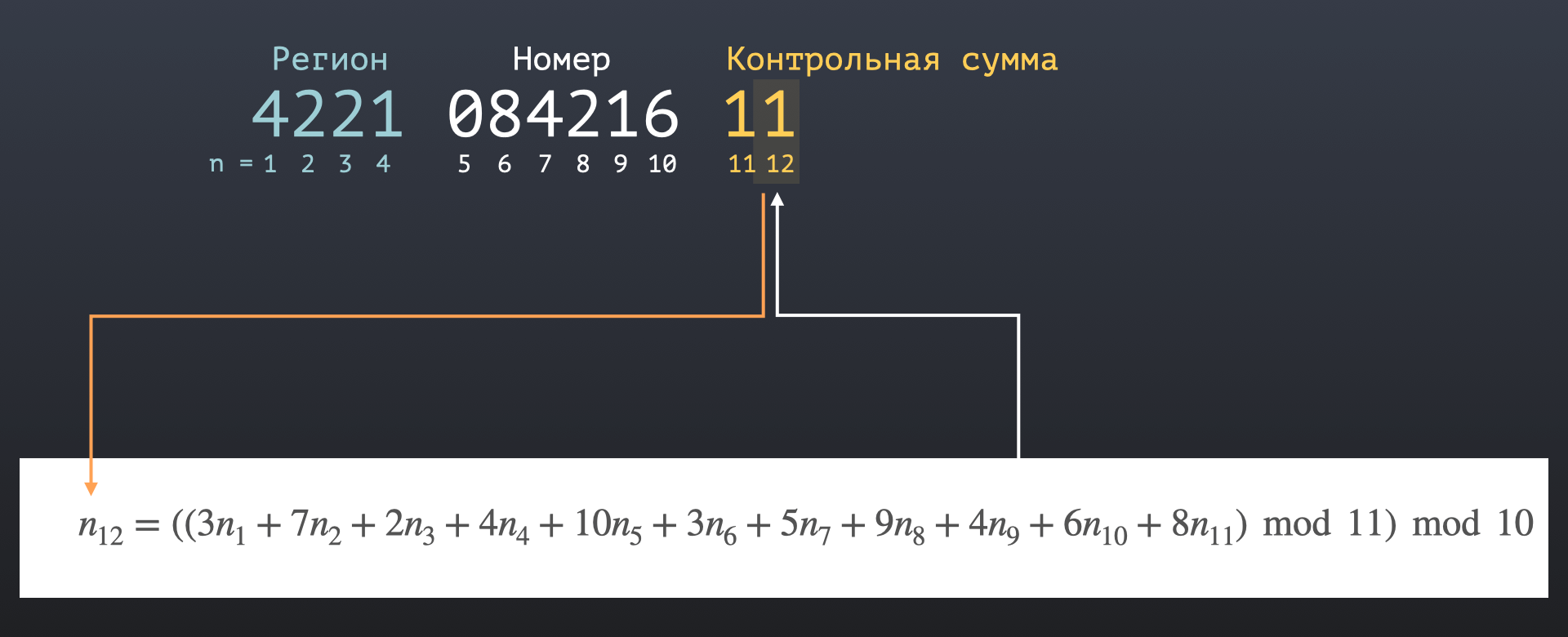
И в целом всё вместе работает так, если мы делаем ошибку в основном номере ИНН, например, написали вместо восьмерки девятку, то контрольные числа также будут вычислены другие. Вместо двух единиц мы получим 6 и 4.

Компьютерная программа сравнит вычисленные контрольные числа с теми, которые мы ввели сами и, если они различаются, она сообщит, что в номере ошибка.

И всё это основано на математических расчетах, в которые входит вычисление остатка от деления. Такие контрольные числа есть в номерах банковских карт, ISBN книг, VIN номере автомобиля, в штрих кодах товаров и других номерах. То есть мы буквально каждый день сталкиваетесь с вычислением остатка от деления, когда пробиваем товар на кассе или вводим номер банковской карты в интернет-магазине.

Остаток от деления повсюду.

11. Прочие алгоритмы

Также остаток от деления используется:

• В простейших алгоритмах расчета случайных чисел.
• При вычислении ячеек для вставки данных в хэш таблицах.
• В алгоритмах проверки числа на простоту.
• Для вычисления ключа по методу Диффи Хэллмана, чтобы обмениваться приватными сообщениями в Телеграме.
• А также в шифровании с открытым ключом, которое используется в интернете на каждом шагу.

Все эти алгоритмы мы подробно разбираем в нашем курсе по Алгоритмам и структурам данных на Python

12. Отрицательный остаток от деления

И напоследок рассмотрим еще один способ применения остатка от деления. В программировании существуют такие алгоритмы, для успешной работы которых, данные должны иметь длину кратную чему-либо.

Представим, что мы обрабатываем информацию блоками по 8 символов. Взяли 8 знаков, обработали, взяли следующую порцию, обработали её.

И нам важно, чтобы все блоки были равной длины. Но часто встречается, что, например, последний блок, содержит меньше символов, чем следует. Скажем три.

Если мы его отправим в наш алгоритм, то произойдет ошибка, потому что он умеет работать только с восьмью символами. Это может быть связано с тем, что алгоритм обрабатывает данные на двоичном уровне и ему нужно определенное количество битов. Как в алгоритме Base64.

Или для того, чтобы улучшить криптостойкость, как в алгоритмах RSA. Или, как в блочном шифровании, получить блоки одинаковой длины.

В общем, для некоторых алгоритмов нам необходимо дополнить строку какими-то символами, часто это символ равенства =

Давайте вычислим, сколько таких символов равно нужно вставить.

Общая длина исходной строки у нас равна 27-и символам и эта строка должна быть кратной 8, то есть нужно дополнить её до 32. При этом 32 у нас нигде не фигурирует.

То есть на входе мы имеем длину строки 27 и размер блока 8. И из них нужно получить величину заполнителя 5.

И собственно формула довольно простая:

8 - (27 % 8)

Часть в скобках говорит, сколько у нас заполнено в последней строке, а далее мы считаем сколько осталось заполнить. Довольно простая арифметика, которая вернет нам 5.

Но давайте подставим в формулу 32, как будто у нас изначально была фраза, кратная восьми:.

8 - (32 % 8)

И подставив 32, по нашей формуле мы получим 8, потому что в скобках будет ноль. То есть формула хорошо работает если текст нужно дозаполнить, но даёт сбой если текст изначально кратен восьми.

Формально сейчас мы должны дополнить его еще одной строкой, которая состоит только из заполнителей. В целом это не страшно, и мы можем скорректировать такое поведение с помощью условий.

Но всё же, есть более изящный способ избежать этого ложного срабатывания. И для этого нужно вычислить остаток от деления отрицательного числа.

Вернем прошлую фразу и напишем такую формулу:

(-27 % 8)

И такое выражение сразу вернет нам 5. А если подставить в формулу 32:

(-32 % 8)

то мы получим ноль, а, следовательно, дополнять фразу не нужно.

И чтобы лучше понять, что происходит, давайте посмотрим на вот таблицу остатков от деления на 8. В ней сверху идут положительные числа, а снизу парные им отрицательные:

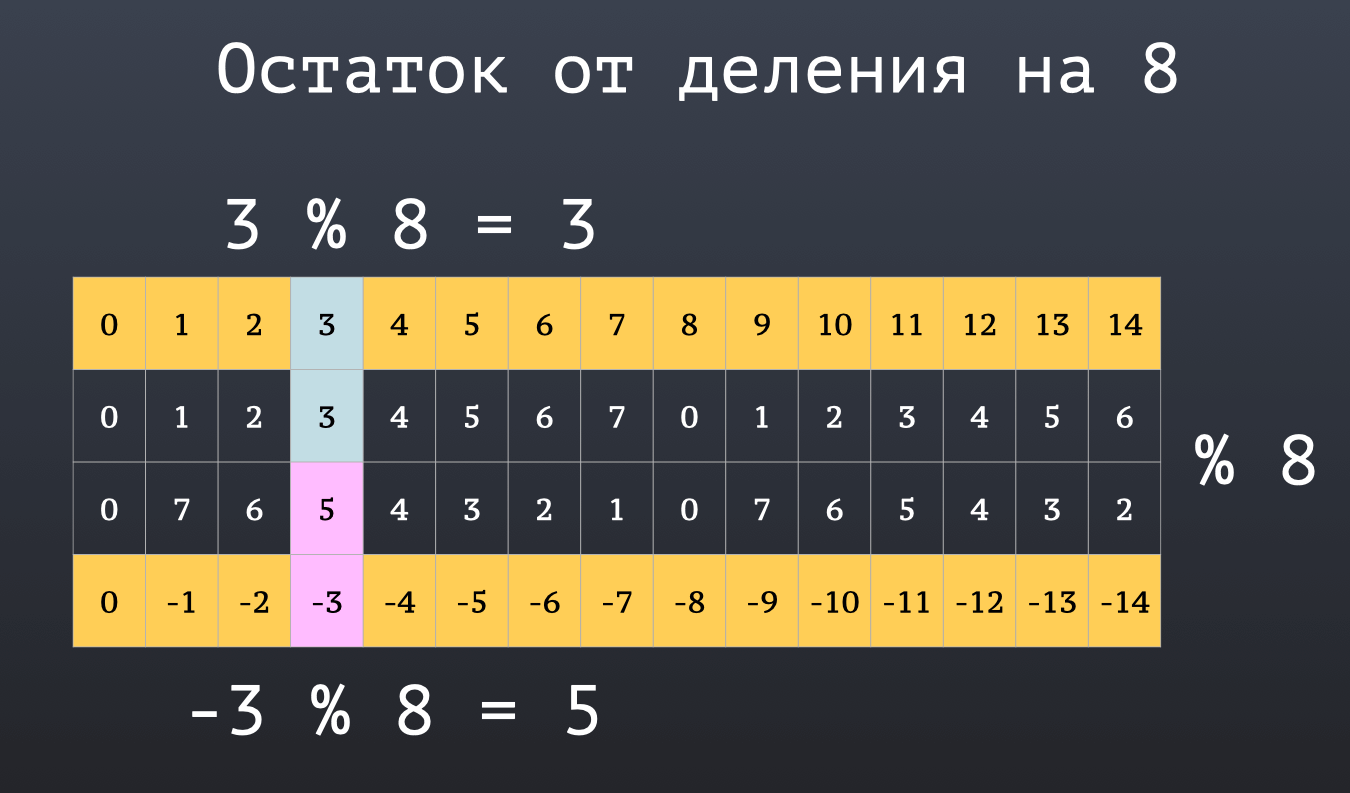
В средних рядах таблица находятся вычисленные остатки от деления для каждого из чисел.

Возьмем, например, 3. Остаток от деления тройки на 8 будет равен трём. Было три яблока и 8 участников, поровну разделить мы не можем, а значит три яблока у нас и осталось.

Снизу идет остаток от деления -3 на 8. И это 5. И пять это то, сколько нам не хватает до того, чтобы добрать до восьми. То есть у нас осталось три яблока и если сейчас мы принесем еще 5, то сможем раздать каждому по одному и у нас ничего не останется.

Или если у нас было 6 яблок, то нам нужно докупить еще два, чтобы всем хватило. А вот если у нас 8 яблок, то нам не нужно ничего докупать. Мы просто раздаём их все и у нас ничего не остается.

В этом и заключается смысл отрицательного остатка от деления.

Что ж, на этом у нас всё и надеемся наше руководство поможем вам лучше писать ваши программы.