Банковское округление в Python
Банковское округление — это один способов округления вещественных чисел, который используется в Python и некоторых других языках программирования.
Проблемы классического округления
Перед тем, как начать новую тему, давайте вспомним правила классического округления, которые вам должны быть знакомы еще со школы. Округлять будем до целого числа́ вот такие чи́сла, с одним знаком после десятичной точки:

Если число в десятичной части содержит четверку или меньше, то оно округляется вниз, а если пятерку или больше, то вверх. 4.4 становится просто 4, 4.5 будет округлено до 5. Уверен вам это хорошо знакомо.
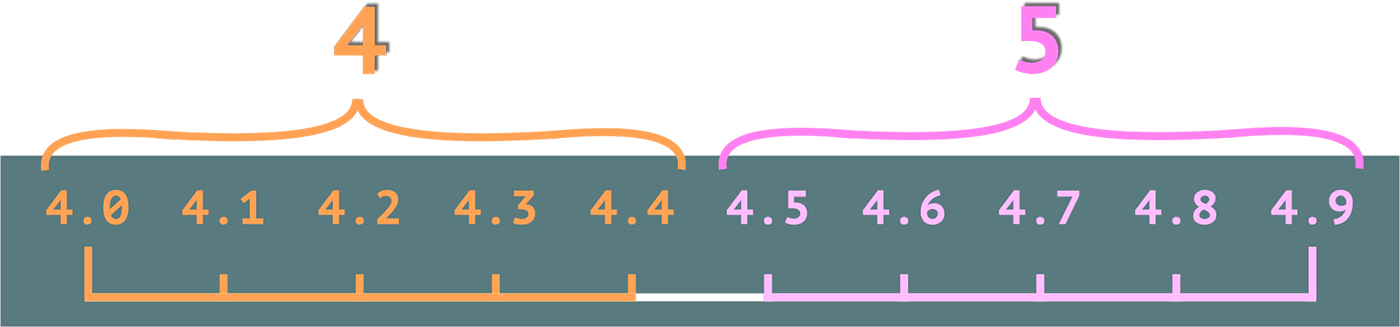
Но давайте посмотрим на такое округление с другой стороны. Реально из 10 представленных чисел 5 будут округлены в большую сторону и только 4 в меньшую. На 4.0 округление никак не повлияет:
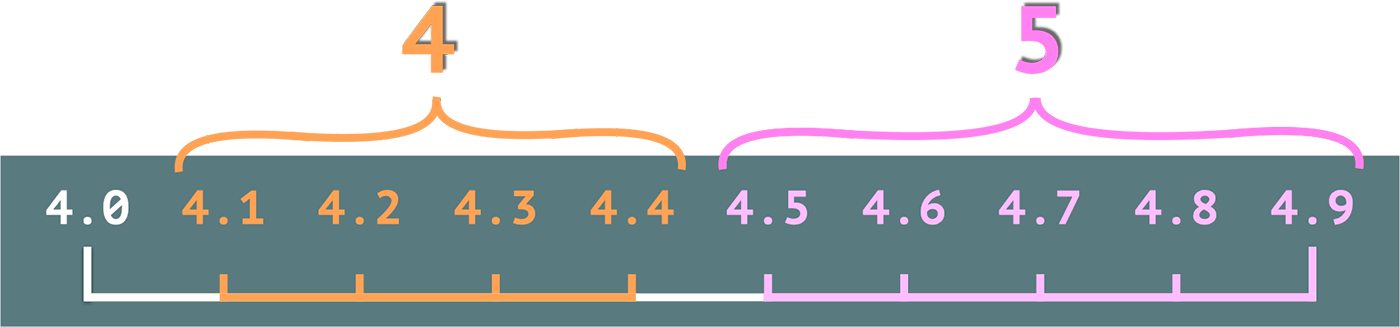
Из-за такого незначительного смещения, на практике при суммировании большого количества округленных чисел появляется погрешность. То есть проблема возникает, когда мы берем какой-то пул чисел, округляем их все, а затем складываем, чтобы получить финальный результат.
Давайте для примера возьмем множество из 1000 значений от нуля до 99.9 с шагом 0.1: 0.1, 0.2, 0.3 и так далее. То есть мы имеем некий набор чисел с равномерным заполнением. Назовем его идеальным:

Если мы сложим все числа без округления, то получим значение 49 950. А если при сложении мы будем округлять каждое значение, то итоговый результат будет равен 50 000.
Разница небольшая, всего в 50, тем не менее она даёт нам погрешность в одну десятую процента. И это в идеальном наборе чисел.
| Набор данных | Без округления | Обычное округление | Банковское округление |
|---|---|---|---|
| Идеальный | 49 950 | 50 000 0.10% |
Теперь давайте также возьмем 1000 чисел, но на этот раз заполнение будет неидеальным. Мы также будем помещать между двумя целыми числами десять дробных значений, но выбирать их будем случайном порядке. Какие-то числа будут повторяться, а какие-то будут пропущены. Например, мы можем встретить два раза 0.1 и при этом не встретить 0.2 и так далее:

Назовём такое множество нормальным. Так как промежуточные значения будут заполняться случайным образом, то и итоговые результаты мы всегда будем получать разные. Дополню табличку данными одного из таких экспериментов:
| Набор данных | Без округления | Обычное округление | Банковское округление |
|---|---|---|---|
| Идеальный | 49 950 | 50 000 0.10% | |
| Нормальный | 49 960 | 50 018 0.14% |
Итак, без округления в сумме я получил 49 960, а с округлением 50 018, что в итоге дало погрешность в 0.14%.
Готовясь к этому видео, я провел несколько экспериментов с разным набором данных и получил разброс погрешности от 0.03 до 0.18%, что в среднем стремится примерно к 0.10% как в идеальном случае, но всё же в зависимости от данных мы можем получить и большие показатели.
При этом надо понимать, что погрешность при округлении — это нормально, ведь мы намеренно отсекаем часть данных, а значит точность будет страдать.
Тем не менее есть сферы, где желательно минимизировать такую погрешность и речь, разумеется, про финансовый и банковский сектор.
Банковское округление
И для того, чтобы снизить погрешность и увеличить точность используют банковское округление, которое также называют конвергентное округление, статистическое, голландское, округление по Гауссу или округление до четного.
И когда мы говорим «до четного» это не просто слова — в них заложен смысл. Давайте возьмем две шкалы: одну от 4 до 5, а вторую от 5 до 6, и применим к этим шкалам банковское округление:
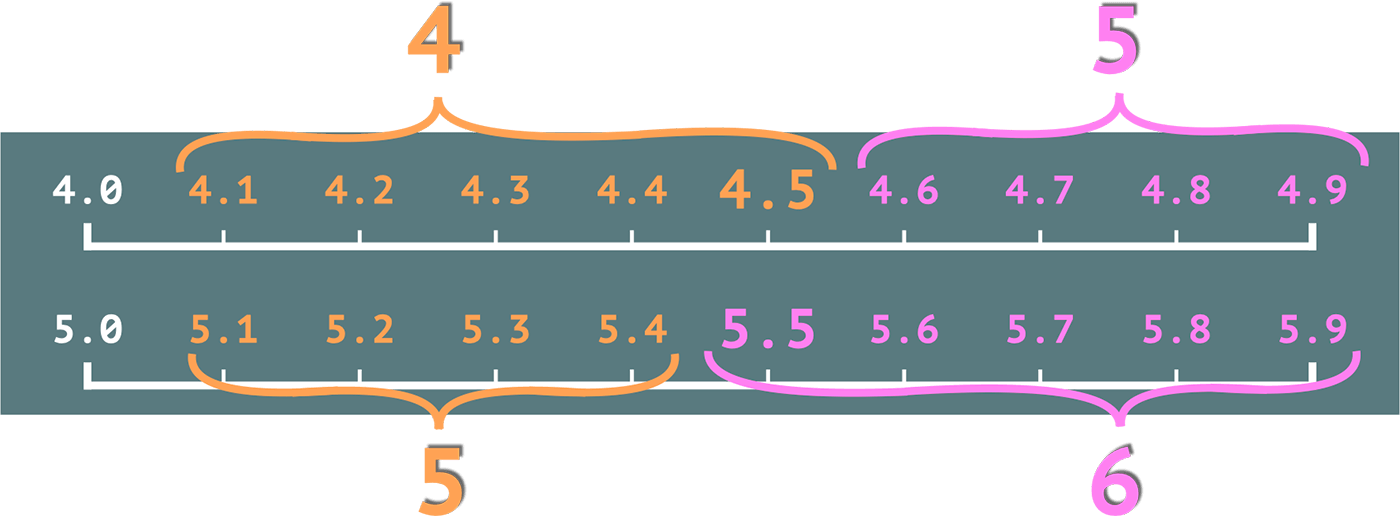
Числа, которые находятся слева и справа от центра, округляются классическим способом. 4.2 до 4-х, 4.9 до 5-и, 5.3 также до 5-и, 5.7 до 6-и — тут всё стандартно.
А вот средние значения: 4.5 и 5.5 надо округлить до ближайшего четного. Так 4.5 будет округлено до 4-х, потому что 4 находится явно ближе, чем 6. А 5.5 будет округлено до 6-и. На этот раз 6 ближе, чем четыре.
И соответственно, если не считать 4.0 и 5.0, на которые округление не действует, то из оставшихся 18 значений, 9 будут округлены в меньшую сторону и 9 в большую. А это значит, что погрешность при суммировании должна уменьшиться. Ведь теперь у нас нет перекоса в какую-либо из сторон.
Давайте посмотрим на нашу таблицу, и я заполнил её значениями, полученными ровно на том же наборе данных, что и для обычного округления:
| Набор данных | Без округления | Обычное округление | Банковское округление |
|---|---|---|---|
| Идеальный | 49 950 | 50 000 0.10% | 49 950 0.00% |
| Нормальный | 49 960 | 50 018 0.14% | 49 964 0.03% |
И обратите внимание, что при идеальном распределении мы имеем нулевую погрешность, а при нормальном, когда числа выбираются случайно, погрешность составляет всего 0.03% вместо 0.14%.
Я также провел несколько экспериментов с разным набором данных, и каждый раз получал погрешность от 0.00% до 0.05%, причем 0.00% или 0.01% встречались гораздо чаще, чем большие значения. Иными словами, точность финального результата оказывалась близка к значению без округления.
Именно из-за этого банковское округление часто используют в финансовой сфере и некоторых языках программирование. В частности, в Python 3 из коробки, а также на платформе .Net.
Что ж, теперь вы больше знаете о том, как устроено банковское округление в Python. Если вы хотите узнать еще больше о том, как работают языки программирования, то подписывайтесь на наш канал, а если хотите научиться программировать на питоне, то ждём нашем курсе.
